Chapter2 Programing Examples

2.1 Problem 1

2.1.1 Kërkesa

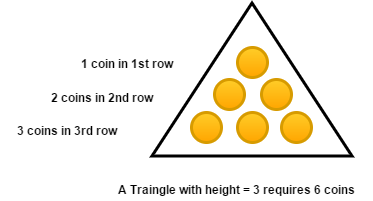
Nqs kemi N monedha dhe i vendosim në formë trekëndëshi, në mënyrë të tillë që:

në rreshtin e parë vendosim 1 monedhë
në rreshtin e dytë vendosim 2 monedha
në rreshtin e tretë vendosim 3 monedha
e kështu me radhë (siç tregohet në figurë)

Sa është lartësia e trekëndëshit më të madh që mund të formohet?

Referenca: https://www.codechef.com/problems/TRICOIN

2.1.1.1 Shembull

$ cat input.txt
3
3
5
7

$ python3 prog.py < input.txt
2
2
3

Testi 1: Nuk mund të formojmë një trekëndësh me lartësi >2, sepse kjo kërkon të paktën 6 monedha.
Testi 2: Nuk mund të formojmë një trekëndësh me lartësi >2, sepse kjo kërkon të paktën 6 monedha.
Testi 3: Nuk mund të formojmë një trekëndësh me lartësi >3, sepse kjo kërkon të paktën 10 monedha.

2.1.2 Zgjidhja 1

T = int(input())
for t in range(T):
     n = int(input())
     l = 0    # lartesia
     s = 0    # sasia e monedhave
     while True:
         s += l + 1
         if s > n:
             break
         else:
             l += 1
     print(l)

2.1.2.1 Sqarime

Fillimisht shënojmë me 0 lartësinë e trekëndëshit dhe sasinë e monedhave që duhet për ta ndërtuar. Pastaj fillojmë ta rrisim lartësinë me nga 1, duke llogaritur edhe sasinë e monedhave që na duhen për ta ndërtuar. Këtë punë e bëjmë deri sa sasia e monedhave mos ta kalojë numrin n që na është dhënë.

2.1.3 Zgjidhja 2

for _ in range(int(input())):
     n = int(input())
     l = s = 0
     while s <= n:
         l += 1
         s += l
     print(l - 1)

Fillojmë ta rrisim lartësinë me nga 1, duke llogaritur edhe sasinë e monedhave që na duhen. Këtë punë e bëjmë deri sa sasia e duhur e monedhave ta kalojë numrin n që na është dhënë. Atere lartësia e mundshme e trekëndëshit është vlera e l-së që sapo kaluam (ku sasia e dhënë e monedhave ishte e mjaftueshme për ta ndërtuar).

2.1.4 Detyra

Shkruani një program që llogarit shumën e shifrave të një numri të dhënë.

Referenca: https://www.codechef.com/problems/FLOW006

2.1.4.1 Shembull

$ cat input.txt
3
12345
31203
2123

$ python3 prog.py < input.txt
15
9
8

2.2 Problem 2

2.2.1 Kërkesa

Në një varg me numra natyrorë \(a_1, a_2, ... , a_n\) gjeni diferencën më të vogël të mundshme midis 2 prej tyre. Dmth gjeni vlerën minimale të \(|a_i - a_j|\) për çdo \(1 \leq i < j \leq n\) .

Referenca: https://www.codechef.com/problems/HORSES

2.2.1.1 Shembull

$ cat input.txt
1
5
4 9 1 32 13

$ python3 prog.py < input.txt
3

2.2.2 Zgjidhja 1

T = int(input())
for t in range(T):
    n = int(input())
    l = list(map(int, input().split()))
    dmin = abs(l[0] - l[1])
    i = 0
    while i <= n-2:
        j = i + 1
        while j <= n-1:
            d = abs(l[i] - l[j])
            if d < dmin:
                dmin = d
            j += 1
        i += 1
    print(dmin)

2.2.2.1 Sqarime

Marrim të gjitha kombinimet e mundshme të i dhe j, gjejmë diferencat midis tyre, dhe ndërkohë gjejmë edhe më të voglën e diferencave.

P.sh. për numrin \(a_1\) bëjmë diferencën me \(a_2, a_3, ... , a_n\), për numrin \(a_2\) bëjmë diferencën me \(a_3, ... , a_n\), e kështu me radhë.

Kjo zgjidhje nuk është dhe aq efiçente sepse për \(n\) numra duhet të bëjmë përafërsisht \(n^2\) veprime (zbritje, krahasime, etj.)

Zgjidhja më poshtë është më e shpejtë.

2.2.3 Zgjidhja 2

T = int(input())
for t in range(T):
    n = int(input())
    l = list(map(int, input().split()))
    l.sort(reverse=True)
    dmin = l[0] - l[1]
    i = 0
    while i <= n-2:
        d = l[i] - l[i+1]
        if d < dmin:
            dmin = d
        i += 1
    print(dmin)

2.2.3.1 Sqarime

Fillimisht i rendisim numrat në rendin zbritës. Pastaj, në vend që të bëjmë diferencën e numrit \(a_i\) me të gjithë numrat pasardhës, mjafton që të bëjmë diferencën e tij vetëm me numrin \(a_{i+1}\), dhe dihet që diferenca me numrat e tjerë pasardhës nuk është më e vogël se kjo (sepse janë më të vegjël se \(a_{i+1}\)).

2.2.4 Detyra

Kemi një varg me numra ku të gjithë numrat përsëriten një numër çift herësh, me përjashtim të njërit i cili përsëritet një numër tek herësh. Të gjendet ky numër.

Referenca: https://www.codechef.com/problems/MISSP

2.2.4.1 Shembull

$ cat input.txt
2
3
1
2
1
5
1
1
2
2
3

$ python3 prog.py < input.txt
2
3

Janë 2 raste testimi, i pari ka 3 numra (njëri nën tjetrin), dhe i dyti ka 5 numra.