Problemi 079

Kërkesa

Një kompani ka një strukture hierarkike si kjo në figurë:

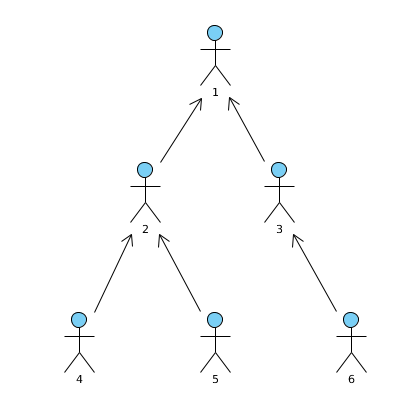
Në krye është pronari i cili nuk varet nga askush, pastaj janë menaxherët, të cilët kanë disa vartës dhe varen nga një menaxher tjetër ose nga pronari, pastaj janë të punësuarit e thjeshtë, të cilët nuk kanë vartës. Kjo strukturë mund të paraqitet duke treguar për çdo person përgjegjësin e tij në këtë mënyrë: 0 1 1 2 2 3 Personi 1 nuk varet nga askush, prandaj përgjegjësi i tij është shënuar me 0. Personat 2 dhe 3 varen nga personi 1, personat 4 dhe 5 varen nga personi 2, dhe personi 6 varet nga personi 3.

Bëni një program që merr paraqitjen e hierarkisë në këtë formë dhe gjen se kush janë punonjësit e thjeshtë.

Referenca: https://www.codechef.com/problems/CHEFDETE

Shembull

$ cat input.txt
2
6
0 1 1 2 2 3
13
0 1 2 3 1 3 5 7 1 9 9 10 11

$ python3 prog.py < input.txt
4 5 6
4 6 8 12 13

Zgjidhja 1

for _ in range(int(input())):
    n = int(input())
    V = [int(i) for i in input().split()]
    P = []
    for i in range(1, n+1):
        if i not in V:
            P.append(i)
    print(*P)

Sqarime

Duhet të gjejmë ata persona që nuk shfaqen në listën e dhënë, sepse ata nuk kanë vartës, pra janë punonjës të thjeshtë. Koha e kësaj zgjidhje është e rendit \(O(N^2)\).

Zgjidhja 2

for _ in range(int(input())):
    n = int(input())
    V = [int(i) for i in input().split()]
    P = []
    V.sort()
    i = 1
    j = 0
    while i <= n and j < len(V):
        if V[j] < i:
            j += 1
        elif V[j] > i:
            P.append(i)
            i += 1
        else:    # V[j] == i
            i += 1
            j += 1
    while i <= n:
        P.append(i)
        i += 1
    print(*P)

Sqarime

Për të gjetur personat që nuk janë në listën e dhënë, fillimisht e renditim listën dhe pastaj bëjmë një kërkim linear në listën e dhënë. Koha e kësaj zgjidhje është \(O(N*ln(N))\) (që është koha për renditjen e listës), e cila është më e mirë se \(O(N^2)\)

Zgjidhja 3

for _ in range(int(input())):
    n = int(input())
    V = [int(i) for i in input().split()]
    P = []
    ka_vartes = [False for i in range(n+1)]
    for i in range(len(V)):
        ka_vartes[V[i]] = True
    for i in range(n+1):
        if not ka_vartes[i]:
            P.append(i)
    print(*P)

Sqarime

Për të gjetur ata persona që nuk kanë vartës, krijojmë një listë me vlera vërtetësie (True/False), dhe shënojmë me True në të personat që kanë vartës.

Koha e kësaj zgjidhje është \(O(N)\), që është më e mirë se \(O(N*ln(N))\).

Detyra

Në koncertin e operas këngëtarja kryesore është një mikja juaj. Ju doni të siguroheni që në fund të shfaqjes e gjithë salla të ngrihet në këmbë dhe të duartrokasë.

Në fillim spektatorët janë të ulur. Çdo spektator ka një nivel turpi. Një spektator me nivel turpi \(S_i\) pret deri sa të paktën \(S_i\) spektatorë të tjerë të jenë çuar në këmbë duke duartrokitur, pastaj çohet edhe ai. Nëse \(S_i = 0\) atere spektatori çohet gjithmonë në këmbë për të duartrokitur, pavarësisht nëse është çuar ndonjë tjetër. Nëse një spektator e ka \(S_i = 2\) atere pret deri sa të çohen të paktën 2 të tjerë, para se të çohet.

Ju e njihni nivelin e turpit të spektatorëve që do shkojnë në koncert dhe mund të ftoni edhe njerëz të tjerë me një nivel turpi të çfarëdoshëm, jo domosdoshmërisht të njëjtë. Sa është numri më i vogël i njerëzve që duhet të ftoni për të garantuar që e gjithë salla do çohet në këmbë.

Referenca: https://code.google.com/codejam/contest/6224486/dashboard#s=p0

Shembull

$ cat input.txt
4
4 11111
1 09
5 110011
0 1

$ python3 prog.py < input.txt
Case #1: 0
Case #2: 1
Case #3: 2
Case #4: 0

Për çdo rast testimi jepet niveli më i lartë i turpit, dhe pastaj jepet një varg numrin e spektatorëve për secilin nivel, duke filluar nga 0. P.sh. “409” do të thotë që 4 persona kanë nivel turpi 0, asnjë me nivel turpi 1, dhe 9 me nivel turpi 2.

Në rastin e parë e gjithë salla do çohet në këmbë pa shtuar asnjë të ftuar tjetër.

Në rastin e dytë, duhet të ftojmë një person me nivel turpi 0, dhe pastaj 9 të tjerët do çohen në këmbë, meqë e kanë nivelin 1.

Në rastin e tretë mund të ftojmë një person me nivel 2 dhe një me nivel 3, ose 2 persona me nivel 2. Të dyja këto raste bëjnë që edhe spektatori me nivel 4 të çohet në këmbë, dhe pas atij edhe spektatori me nivel 5.